转置卷积与卷积的理解
转置卷积与卷积的理解,本文将介绍:
- 转置卷积含义与矩阵形式
- 转置卷积的一种简单理解
- pytorch 转置卷积参数的理解及其Shape的公式推导
- 卷积与数学上的卷积,卷积核旋转180度
阅读前提:
- 理解深度学习中普通卷积的概念与shape的计算公式
- 了解深度学习框架pytorch卷积api的调用
- 了解卷积的矩阵运算形式
转置卷积含义与矩阵形式
文档: A guide to convolution arithmetic for deep learning 介绍了转置卷积一个概念:The need for transposed convolutions generally arises from the desire to use a transformation going in the opposite direction of a normal convolution, i.e., from something that has the shape of the output of some convolution to something that has the shape of its input while maintaining a connectivity pattern that is compatible with said convolution.
翻译一下就是:一个普通卷积的反向操作,已知一个卷积操作L,它输入是A,输出是B,现在需要将B重新变回具有与A形状线相同的C,并且C与A依然保持一种与卷积操作L相容(一致性)的连接特性。注意:C与B只是形状相同,但是数值一般是不同的。 另外转置卷积的作用:以一个已经编码的layer进行解码,或者将特征图映射到高维空间(or project feature maps to a higher-dimensional space.)
转置卷积也有其他的概念,而转置卷积的名称与使用矩阵运算来计算卷积有关(Convolution as a matrix operation):
以图2.1所表示的卷积为例。如果将输入和输出从左到右、从上到下展开成向量,那么卷积可以表示为一个稀疏矩阵\(C\),其中非零元素是卷积核的元素\(W(i,j)\)(其中 \(i\) 和 \(j\) 分别是卷积核的行和列):
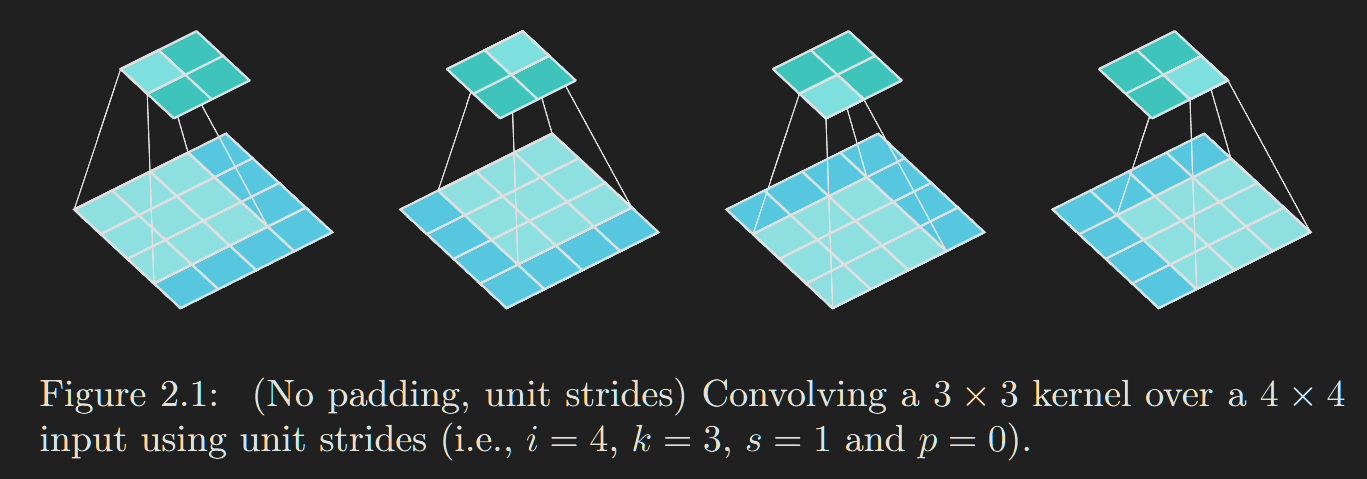

这个线性运算将输入矩阵展平为一个16维向量\(X\),并产生一个4维向量\(Z\),之后被重新整形为2×2的输出矩阵。利用这种表示方法,反向传播很容易通过转置\(C\)来获取;换句话说,误差通过将损失与\(C^T\)相乘来进行反向传播。该运算以一个4维向量作为输入,并产生一个16维向量作为输出,其连接模式与\(C\)的构造方式兼容。 值得注意的是,核\(W\)定义了用于正向和反向传播的矩阵\(C\)和\(C^T\)。梯度反向传播的过程中,在计算输入\(X\)的梯度时,是通过该4维向量\(Z\)的梯度(也是反向传播过来的)与\(C^T\)相乘来计算的。
转置卷积是相对原卷积来说的。原卷积的不同卷积方式,对应的转置卷积也是不一样的。转置卷积可以通过普通的卷积来实现。
具体的实现方式参考: A guide to convolution arithmetic for deep learning ,在第4章有详细的介绍。
原卷积如果是No zero padding, unit strides,那么转置卷积将采用full-conv,例如:
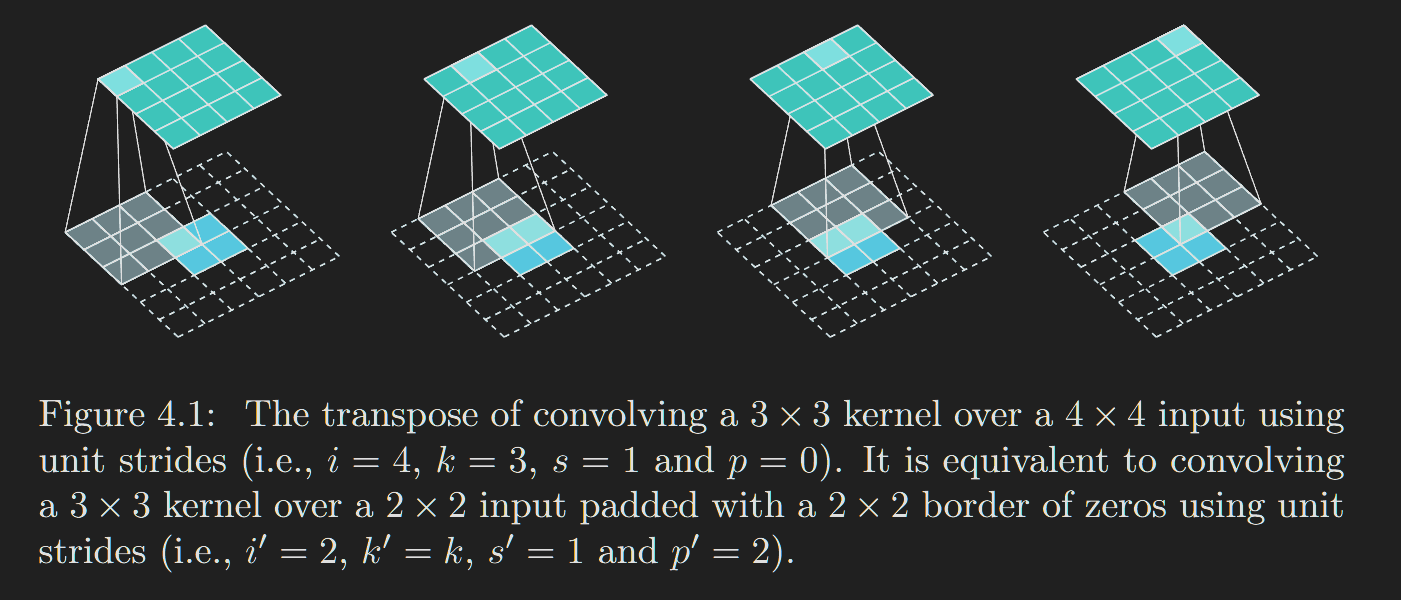
图4.1 解释:
Relationship 8. A convolution described by s = 1, p = 0 and k
has an associated transposed convolution described by k′= k, s′= s
and p′= k −1 and its output size is o′= i′+ (k −1).
其中i’ = (i-k+2*p)/s + 1
值得注意:pytorch 的转置卷积默认是full-conv,pytorch 转置卷积将再第3节介绍。
另外的参考:https://zh-v2.d2l.ai/chapter_computer-vision/transposed-conv.html 其中有解释转置卷积的名称由来:抽象来看,给定输入向量\(\mathbf{x}\)和权重矩阵\(W\),卷积的前向传播函数可以通过将其输入与权重矩阵相乘并输出向量\(\mathbf{y}=\mathbf{W}\mathbf{x}\)来实现。 由于反向传播遵循链式法则和\(\nabla_{\mathbf{x}}\mathbf{y}=\mathbf{W}^\top\),卷积的反向传播函数可以通过将其输入与转置的权重矩阵\(\mathbf{W}^\top\)相乘来实现。 因此,转置卷积层能够交换卷积层的正向传播函数和反向传播函数:它的正向传播和反向传播函数将输入向量分别与\(\mathbf{W}^\top\)和\(\mathbf{W}\)相乘。
转置卷积的一种简单理解
文档
https://zh-v2.d2l.ai/chapter_computer-vision/transposed-conv.html
介绍了一种简单的转置卷积理解方式:
输入\(i\) 是[[0,1],[2,3]], 转置卷积核也为:[[0,1],[2,3]](注意:该卷积与pytorch的实现方式不一样,但这是另外一种理解,而且与pytorch的转置卷积api计算结果一致)
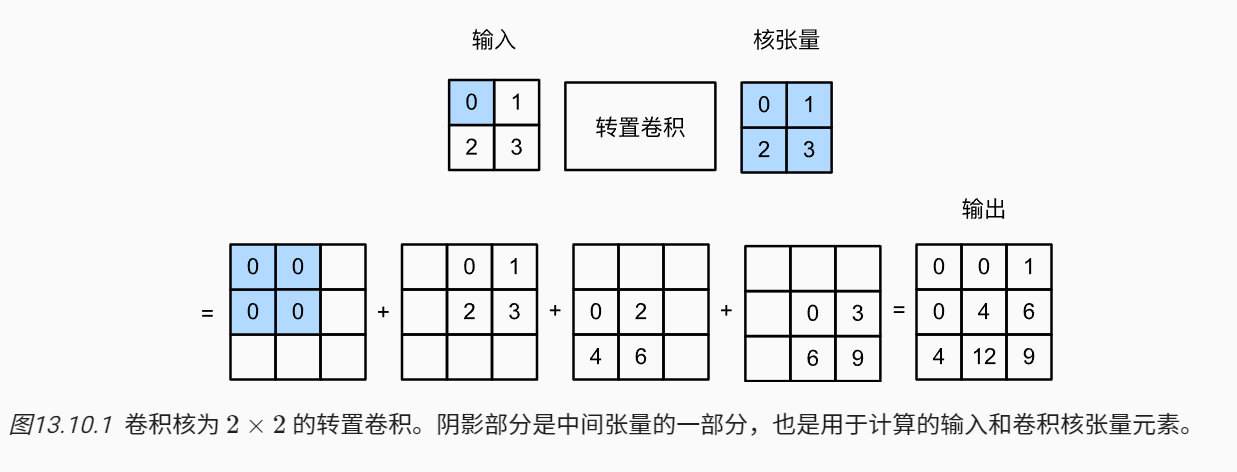
该转置卷积设步幅为1且没有填充。输入张量中的每个元素都要乘以卷积核,然后产生了4个中间结果,然后加起来得到就是转置卷积的结果。
注意:图13.10.1转置卷积对应的原卷积的参数是:stride = 1, padding = 0。这样输出的shape : i' = (i-k+2*padding)/stride + 1 == i-(k-1),而转置卷积的目的是在形状上将\(i’\)恢复为 \(i\) ,且保持卷积的一种一致性。可以用一下代码实现,定义函数trans_conv,输入矩阵\(X\)和卷积核矩阵\(K\)实现基本的转置卷积运算:
def trans_conv(X, K):
h, w = K.shape
Y = torch.zeros((X.shape[0] + h - 1, X.shape[1] + w - 1))
for i in range(X.shape[0]):
for j in range(X.shape[1]):
Y[i: i + h, j: j + w] += X[i, j] * K
return Y
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
trans_conv(X, K)
输出:
tensor([[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]])
当输入X和卷积核K都是四维张量时,我们可以使用高级API(pytorch)获得相同的结果。
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)
结果也是一样:
tensor([[[[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]]]], grad_fn=<ConvolutionBackward0>)
更详细的内容,下面两个链接不错: 转置卷积 Transposed Convolutions explained with… MS Excel!
pytorch 转置卷积参数的理解及其Shape的公式推导
pytorch 转置卷积 的文档: torch.nn.ConvTranspose2d
另外下面这个文档比较重要,也是本文主要的参考文章 A guide to convolution arithmetic for deep learning
pytorch 转置卷积shape的计算公式
pytorch 的转置卷积包含很多参数,它的基本含义是,如果转置卷积使用原卷积相同的参数,那么转置卷积结果的shape与原卷积的输入保持一致, 这个概念很重要。 pytorch 转置卷积的函数签名:
CLASS torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode='zeros', device=None, dtype=None)
pytorch转置卷积输出的shape是有计算公式的:
$$H_{out} = (H_{in} - 1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0]\times (\text{kernel_size}[0] - 1) + \text{output_padding}[0] + 1 $$
$$W_{out} = (W_{in} - 1) \times \text{stride}[1] - 2 \times \text{padding}[1] + \text{dilation}[1] \times (\text{kernel_size}[1] - 1) + \text{output_padding}[1] + 1$$
pytorch 转置卷积 的计算过程
接下来介绍该算式的含义。 为了理解转置卷积,需要结合原卷积来理解,下面一起考虑原卷积和对应的转置卷积:
假设原卷积输入特征图 \(H_{in}\)= \(i\) ,卷积核设置(kernel= \(k\) , stride= \(s\) , padding= \(p\) , dilation= \(d\) 等)输出的特征图为 \(i’\) 。对应的转置卷积,当给一个特征图 \(i’\), 以及给定相同的卷积核设置(stride=\(s\), padding=\(p\), dilation= \(d\) 等),在pytorch中这个设置将会输出特征图形状 \(o_t\) 与特征图 \(i\) 一致(值是不保证相同的,值通常也不相同)。
接下来我们分为2步1进行转置卷积操作:
- 第一步:对输入的特征图 \(i’\) 进行一些变换,例如:元素之间插入0,特征图周围进行padding,得到新的特征图 \(\tilde{i’}\)
- 第二步:在新的特征图上做普通卷积 (kernel=\(k\), stride=1,dilation=\(d\) 等),得到的结果 \(o_t\) 就是转置卷积的结果,就是我们要求的结果。
第一步,对输入的特征图进行一些变换
pytorch 转置卷积有一些重要的默认设置: stride=1, padding=0, dilation=1
其中stride 控制互相关的步幅(原文是:controls the stride for the cross-correlation.)。它对应的是原卷积的stride,例如:原卷积的stride 是2,那么转置卷积的stride也设置2,如图4.6所示。但是转置卷积处理与原卷积不同:在特征图a元素中间隔插入(stride-1)=1 个零元素。这么做的原因是考虑一种原卷积与转置卷积具有某种相同的连接模式, 这个后面再解释。
转置卷积的padding 控制方式与原卷积看似比较奇怪,直接看pytorch的处理方式:不考虑dilation的情况下,dilation 后面再解释,转置卷积paddding计算公式为:(kernel_size - 1) - padding ,例如:转置卷积 kernel_size=3,padding=1, 那么实际的padding为 (3-1)-1 = 1, 注意这里的padding 指的是单边padding的大小。如果考虑两边要乘2。
这里有个规律2 : 当原卷积padding=0时,转置卷积: padding=(kernel_size -1), 这种padding表明转置卷积是一种全卷积(full-convolution), 也称为:full padding。当原卷积是全卷积时,考虑上面转置卷积paddding计算公式,那么转置卷积的padding=0,即: padding=(kernel_size-1) - (kernel_size-1)=0 。当然还有half-padding: 原卷积与转置卷积此时有相同的padding: \(\lfloor (k -1)/2 \rfloor\)。
转置卷积 padding 的控制方式同样要考虑 dilation 的情况 (dilation 参考 2 中 5.1 Dilated convolutions)。转置卷积paddding公式为:dilation * (kernel_size - 1) - padding ,例如:转置卷积 kernel_size=3,padding=1 , dilation=1, 那么实际的padding为 2*(3-1)-1 = 3。直观理解dilation(空洞卷积)就是某种程度上卷积核变大了,那么对应的padding也要变大。才能保证原卷积与转置卷积具有某种相同的连接模式。
注意:dilation * (kernel_size - 1) - padding, 这里padding 是指原卷积的padding, 也就是说pytorch 中输入的参数:strides, padding 都是指原卷积的padding。
第一步:对输入的特征图 \(i’\) 进行一些变换得到\(\tilde{i’}\) 就介绍到这里,虽然不止这些,但对理解pytorch的转置卷积输出shape的计算公式差不多够了。由参数strides和padding变换得到\(\tilde{i’}\)大小为:$$H_{\tilde{i’}}= i’ + (i’-1) * (s-1) + 2[d*(k-1)-p]$$
转置卷积、padding 之所以这样处理是有原因的2,原卷积与转置卷积具有某种相同的连接模式的直观理解:
One way to understand the logic behind zero padding is to consider the connectivity pattern of the transposed convolution and use it to guide the design of the equivalent convolution. For example, the top left pixel of the input of the direct convolution only contribute to the top left pixel of the output, the top right pixel is only connected to the top right output pixel, and so on.
To maintain the same connectivity pattern in the equivalent convolution it is necessary to zero pad the input in such a way that the first (top-left) application of the kernel only touches the top-left pixel, i.e., the padding has to be equal to the size of the kernel minus one.
翻译一下就是:理解零填充背后的逻辑的一种方法是考虑反卷积的连接模式,并使用它来指导等价的卷积(转置卷积实际的实现方式)设计。例如,直接卷积输入的左上角像素仅对输出的左上角像素有贡献,右上角像素仅连接到右上角输出像素,依此类推。以图4.1为例,为了在等价卷积(转置卷积实际的实现方式)中保持相同的连接模式,需要以零填充输入,使得核的第一次(左上角)卷积仅接触左上角像素,即填充必须等于核大小减一(仅仅是图4.1的情况,)。
例如:
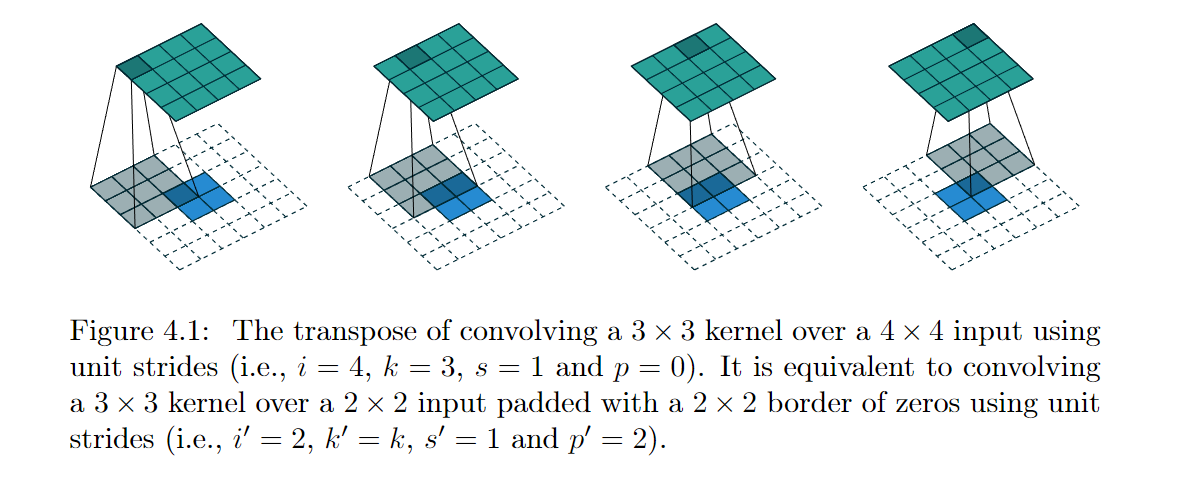 图4.12是一个转置卷积的例子,原卷积是:
图4.12是一个转置卷积的例子,原卷积是:3*3 kernel over a 4*4 input using unit strides(i.e., i = 4, k=3, s=1 and p=0), 转置卷积的等价卷积是:3*3 kernel over a 2*2 input , padding=2, strides = 1. (i.e., i'=2, k'=k=3, s'=1, and p'= 2 = (k-1) - p
总的来说,输入的特征图 \(i’\) 进行一些变换之所以要这样处理(stride 、padding等)是为了保持同样的连接性:这是指从A到B(AB分别表示卷积前和卷积后的特征图),如果A中一个位置与B中一个位置通过kernel有关系,那么在卷积核逆卷积中有相同的连通。1
另外一个例子:
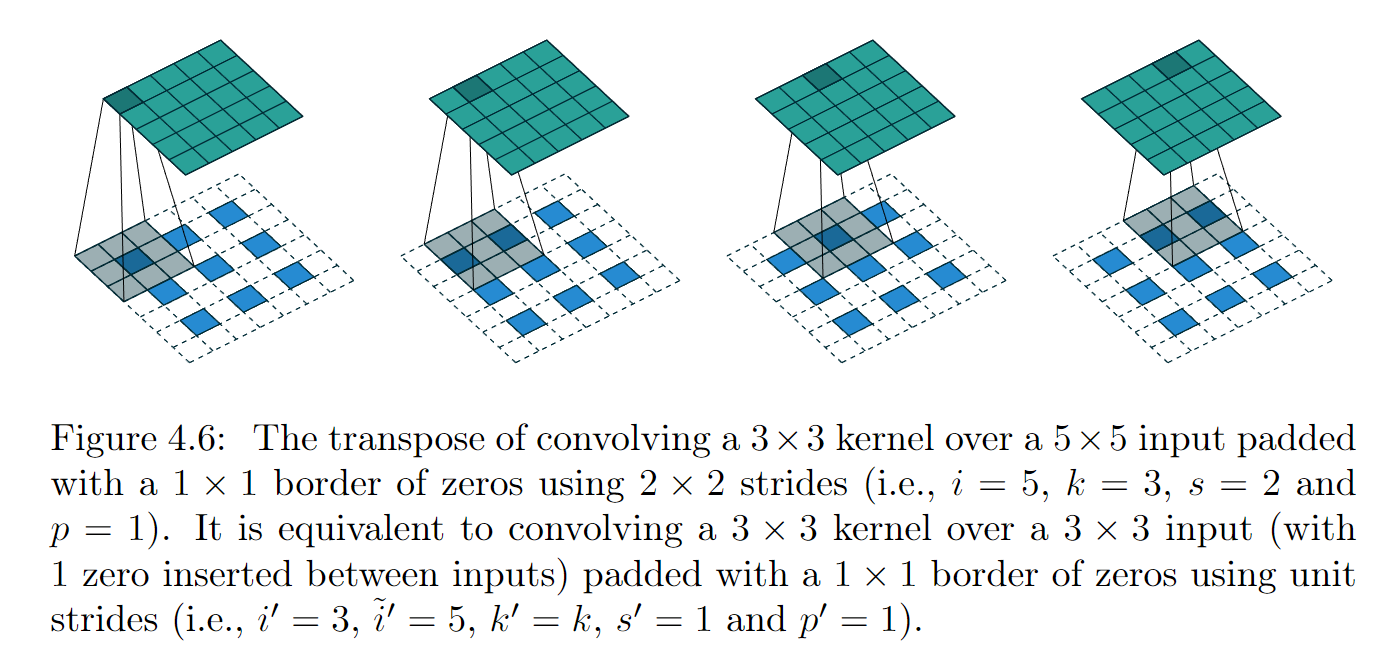 图4.62
图4.62
第二步,对变换得到特征图进行普通的卷积
第二步思路比较简单,对变换得到\(\tilde{i’}\) 进行普通的卷积,kernel = k, strides=1, padding=0, dilation=d, 由于考虑dialation, 等效的卷积核(感受野)大小为:\(k+(k-1)*(d-1)\)
由第一步可知:由参数strides和padding变换得到特征图\(\tilde{i’}\)大小为: $$H_{\tilde{i’}}= i’ + (i’-1) * (s-1) + 2[d*(k-1)-p]$$
转置卷积shape计算:\(o_t=\frac{H_{i’} - [k+(k-1)*(d-1)]}{1} + 1\)
公式化简一下就是:\(o_t=(i’-1)s - 2p + d(k-1) + 1\)
但是pytorch 的计算公式是: $$H_{out} = (H_{in} - 1) \times \text{stride}[0] - 2 \times \text{padding}[0] + \text{dilation}[0]\times (\text{kernel_size}[0] - 1) + \text{output_padding}[0] + 1 $$ 对比一下发现少了一项:\(\text{output_padding}[0]\) \(\text{output_padding}[0]\) 这一项是为了解决转置卷积同一个 \(i’\) 对应多个 \(i\) 的问题,即原卷积的输出\(i’\) 可能因为不同的strides、padding设置而对应多个不同shape的 \(i\) , 这时候需要添加额外的参数\(\text{output_padding}[0]\)使得转置卷积还原为一个特定的 \(i\) 的形状,它的操作是单边补零的,pytorch 参数解释:Additional size added to one side of each dimension in the output shape. Default: 0。
例如:
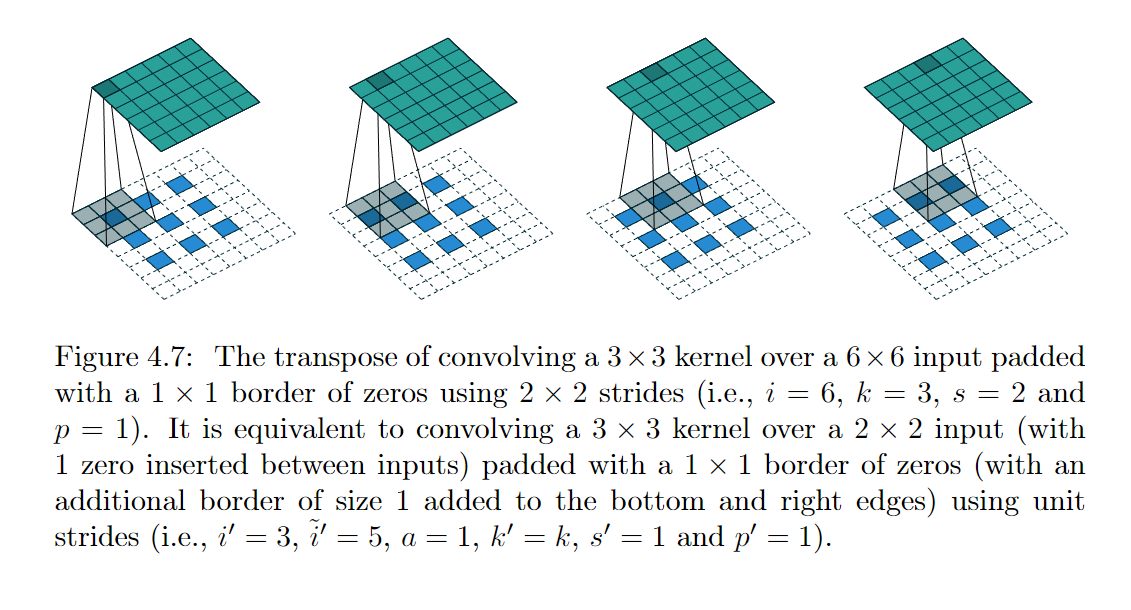
于是加上\(\text{output_padding}\)的转置卷积shape计算公式:
\(o_t=(i’-1)*s -2p + d(k-1) +\text{output_padding} +1\) 。它与pytorch 的给出的公式一致。
参考: 转置卷积 Transposed Convolutions explained with… MS Excel!
卷积与数学上的卷积
pytorch 的转置卷积的核旋转了180度
将第一节(转置卷积的直观理解)与第二节(pytorch 转置卷积参数的理解,以及转置卷积Shape的公式推导)进行对比,你会发现这里两种操作完全不同,但是得到了相同的结果。这其中必然有某种联系。
还是考虑第一节的例子:
 图13.10.1
采用pytorch 的做法,第一步先将输入\(i’\) (转置卷积的输入,另外\(i\)表示的是原卷积的输入)进行变换,假设原卷积的参数是:kernel = 2, strides = 1,padding=0。
strides =1, 输入\(i’\) 元素之间不需要插入0
padding=0, 实际的padding = (k-1)-p = (2-1)-0 = 1
那么变换后的 \(\tilde{i’}\) (转置卷积的输出):
图13.10.1
采用pytorch 的做法,第一步先将输入\(i’\) (转置卷积的输入,另外\(i\)表示的是原卷积的输入)进行变换,假设原卷积的参数是:kernel = 2, strides = 1,padding=0。
strides =1, 输入\(i’\) 元素之间不需要插入0
padding=0, 实际的padding = (k-1)-p = (2-1)-0 = 1
那么变换后的 \(\tilde{i’}\) (转置卷积的输出):

然后进行第二步:对变换后的 \(\tilde{i’}\) 进行普通的卷积:k=2, s=1, p=0
k =[[0,1],[2,3]]
看起来不复杂,可以直接手算,得到卷积的结果:\(o_1\) = [[0,3,2],[6,14, 6],[2,3,0]],这与图13.10.1的输出完全不同。
但是你如果用pytorch的转置卷积api 算一下,又会发现结果与图13.10.1的输出完全一致。例如:
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
X, K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2)
tconv = nn.ConvTranspose2d(1, 1, kernel_size=2, bias=False)
tconv.weight.data = K
tconv(X)
输出:
tensor([[[[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]]]], grad_fn=<ConvolutionBackward0>)
那么是哪里出了问题呢?
问题在第二步,对变换后的 \(\tilde{i’}\) 进行普通的卷积时,卷积核需要旋转180度。新的卷积核是:
k_new = [[3.0, 2.0], [1.0, 0.0]], 对变换后的 \(\tilde{i’}\) 进行普通的卷积(k=2, s=1, p=0)。结果是:\(o_2\) = [[0,0,1],[0,4, 6],[4,12,9]] 这就与pytorch的计算一致了。
这里用pytorch Conv2d (普通卷积api) 进行了验证:
import torch
from torch import nn
X = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
T_K = torch.tensor([[3.0, 2.0], [1.0, 0.0]])
X, K, T_K = X.reshape(1, 1, 2, 2), K.reshape(1, 1, 2, 2), T_K.reshape(1, 1, 2, 2)
def nn_conv2d(im, kernel):
# 用nn.Conv2d定义卷积操作
conv_op = nn.Conv2d(1, 1, kernel_size=2, stride=1, padding=1, bias=False)
# 给卷积操作的卷积核赋值
conv_op.weight.data = kernel
# 对图像进行卷积操作
conv_res = conv_op(im)
return conv_res
res = nn_conv2d(X, K)
print(res)
res2 = nn_conv2d(X, T_K)
print(res2)
结果是:
tensor([[[[ 0., 3., 2.],
[ 6., 14., 6.],
[ 2., 3., 0.]]]], grad_fn=<ConvolutionBackward0>)
tensor([[[[ 0., 0., 1.],
[ 0., 4., 6.],
[ 4., 12., 9.]]]], grad_fn=<ConvolutionBackward0>)
可以看到nn_conv2d(X, T_K)函数输出了正确结果,这说明nn.Conv2d 没有对卷积核进行180度旋转,但是转置卷积nn.ConvTranspose2d对卷积核进行180度旋转。
旋转卷积核后与第一节中的计算结果保持一致,第一节中的计算简单描述就是:每个元素直接与卷积核相乘,然后将所有的中间结果进行叠加。当然这种操作还涉及到strides大于1的情况3,这里就不解释了。
数学上定义的卷积
其实原本数学上的卷积就是要将卷积核进行旋转180度,数学上的卷积与图13.10.1 的操作应该存在着联系。即:图13.10.1 的操作 与使用翻转180度的[[0,1],[2,3]]对 \(\tilde{i’}\) 进行卷积是等价的。
这种联系不打算深究。接下来本文打算给出一些直观的例子。
在此之前先解释一下数学上的卷积是怎么回事。
在数学上,连续形式的卷积定义如下:
设 \(f(x)\) 和 \(g(x)\) 是在实数域上的两个可积函数,定义它们的卷积 \(h(x)\) 为:
\(h(x) = (f*g)(x) = \int_{-\infty}^{\infty} f(\tau)g(x-\tau) d\tau\)
其中,\(*\) 表示卷积操作,\(h(x)\) 表示卷积的输出,\(f(x)\) 和 \(g(x)\) 分别表示卷积的输入函数,\(\tau\) 是积分变量。
卷积的计算过程可以理解为将 \(f(x)\) 和 \(g(x)\) 进行平移、翻转、相乘和积分的过程。具体来说,对于 \(g(\tau)\),首先将其进行翻转得到 \(g(-\tau)\),然后将其在 \(x\) 轴上平移 \(x\) 个单位得到 \(g(x-\tau)\),然后再与 \(f(\tau)\) 相乘,并对 \(\tau\) 进行积分,最终得到卷积的输出 \(h(x)\)。
图像的卷积是离散形式,离散形式的卷积定义如下:
设 \(f[n]\) 和 \(g[n]\) 是在整数域上的两个离散序列,定义它们的卷积 \(h[n]\) 为:
\(h[n] = (f*g)[n] = \sum_{m=-\infty}^{\infty} f[m]g[n-m]\)
离散形式与连续形式类似,当确定一个n后,计算 \(\sum_{m=-\infty}^{\infty} f[m]g[n-m]\) 时,不是积分而是求和。如果与图像的卷积类别。每个n 对应卷积核的一次平移,计算\(\sum_{m=-\infty}^{\infty} f[m]g[n-m]\)对应一次将卷积核旋转180度然后对应元素直接进行相乘求和。
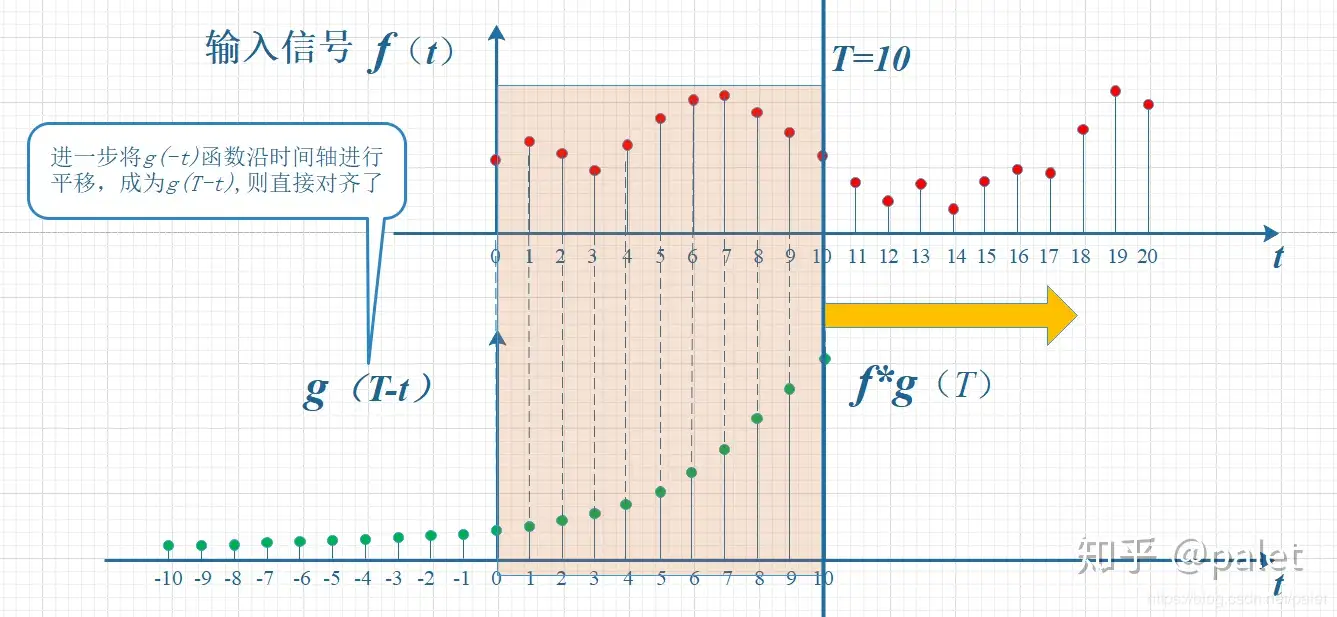
卷积可以用概括为:翻转、平移、相乘再求和
先对g函数进行翻转,相当于在数轴上把g函数从右边褶到左边去,也就是卷积的“卷”的由来。
然后再把g函数平移到n,在这个位置对两个函数的对应点相乘,然后相加,这个过程是卷积的“积”的过程。4
例如:
 更具体的例子可看
如何通俗易懂地解释卷积? - palet的回答 - 知乎
中的
更具体的例子可看
如何通俗易懂地解释卷积? - palet的回答 - 知乎
中的信号分析、丢骰子与图像处理的例子。
多项式系数卷积与意义
接下来是一个一维矩阵的卷积,希望有更直观数学意义5,这里只是给出一种直观的感觉,不解释这么做的原因,因为笔者也不太清楚。
考虑两个多项式函数:
\(y=3x+2\)
\(y=2x^2+3x-1\)
将这两个函数相乘:\(y=(3x+2)(2x^2+3x-1)= 6x^2+13x+3x-2\)
可以将这两个函数的系数按x的阶数从大到小考虑为两个矩阵,然后进行卷积:
\(y=3x+2\) 的系数矩阵:i=[3,2]
\(y=2x^2+3x-1\) 的系数矩阵:K=[2, 3, -1],当成卷积核。旋转180度后卷积核:T_K=[-1, 3, 2]
将两个矩阵进行卷积:
- 首先将系数矩阵
[3,2]进行padding:[0,0,3,2,0,0], padding= 2 = kernel_size -1 = 3 - 1。 - 移动卷积核:T_K=
[-1, 3, 2]进行计算: - 例如:
| 0 | 0 | 3 | 2 | 0 | 0 |
|---|---|---|---|---|---|
| -1 | 3 | 2 |
| 0 | 0 | 3 | 2 | 0 | 0 |
|---|---|---|---|---|---|
| -1 | 3 | 2 |
| 0 | 0 | 3 | 2 | 0 | 0 |
|---|---|---|---|---|---|
| -1 | 3 | 2 |
| 0 | 0 | 3 | 2 | 0 | 0 |
|---|---|---|---|---|---|
| -1 | 3 | 2 |
最后结果是:[2*3, 3*3+2*2, 2*3-1*3, -1*2] = [6, 13, 3, 2] 恰好是\(6x^2+13x+3x-2\) 的系数。感觉翻转180度进行卷积与多项式的计算有关联,计算的结果是有意义的,这些系数是\(x^n\)的系数,或者说是某种特征的系数。
另外考虑另外一种实现方式,类似于图13.10.1,也类似于\(y=(3x+2)(2x^2+3x-1)= 6x^2+13x+3x-2\)的化简过程:
将矩阵:i=[3,2]的每个元素与系数矩阵:K=[2, 3, -1]相乘,例如:
[3]*[2,3,-1] -> [6, 9, -3]
[2]*[2,3,-1] -> [4, 6, -2]
然后将这两个中间结果矩阵按下面的形式相加,最后也得到了同样的系数。
| 6 | 9 | -3 | |
|---|---|---|---|
| 4 | 6 | -2 | |
| 6 | 13 | 3 | -2 |
思考:这里的中间结果相加对齐了两个元素(考虑\(x^n\)的合并),而图13.10.1 中间结果只是对齐了一个元素,这是为什么?可能与卷积核的大小有关,如果卷积核是4x4 那么中间结果相加是不是要对齐3个元素?